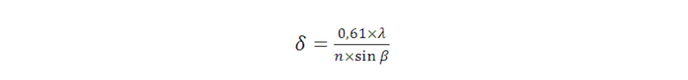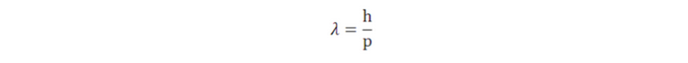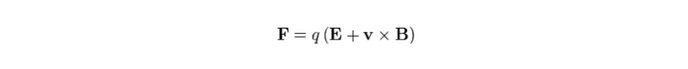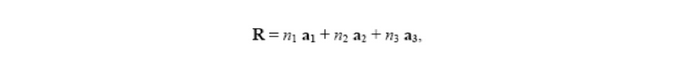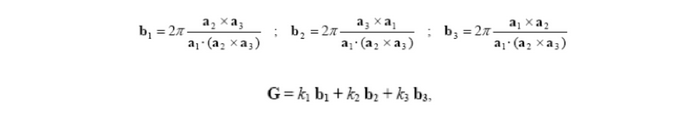Introducción
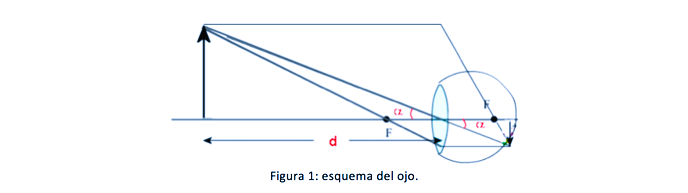
Cuanto más acercamos un objeto al ojo, mayor es el ángulo aparente. Pero existe una distancia mínima, el punto próximo (25 cm), por delante de la cual no se ve nítidamente el objeto. En este punto la imagen llega a su máximo tamaño en la retina y todavía la percibimos con nitidez. Para un ojo normal, un objeto situado a la distancia x = 0,25 m –punto próximo- lo ve el ojo bajo un ángulo aparente máximo. El cristalino es una lente convergente (figura 1), así que los rayos que pasen por el centro de la lente no se desviarán y los que pasen por la focal llegarán paralelos al eje óptico.
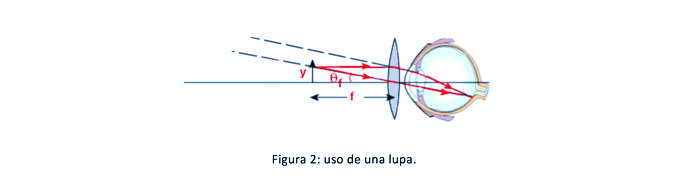
Así queda claro que si queremos observar objetos los bastante pequeños, el ojo no será suficiente. En este sentido, se pueden utilizar microscopios ópticos o lupas (figura 2).
Si el objeto se sitúa en el foco de la lente, el ojo situado en cualquier posición detrás de la lupa ve la imagen sin acomodación. La imagen que produce la lupa se forma en el infinito pero la imagen del sistema lupa + ojo se forma en la retina. El aumento lateral de la lupa vendrá dado por la distancia del punto próximo (como se ha dicho, unos 25cm) a la focal de la lupa.
¿Podemos hacer esta focal infinitamente pequeña para tener un aumento infinitamente grande? ¿Qué limita la resolución de los microscopios ópticos? Justamente el hecho de que trabajamos con fotones.
Recordemos el principio de Huygens:
“Todos los puntos a lo largo de un frente de ondas actúan como emisores puntuales. Por lo tanto, cuando una onda se encuentra con una barrera con una pequeña apertura, todos los emisores se ven bloqueados excepto uno, y la luz que pasa por la apertura se comporta como un emisor puntual, de forma que la luz sigue en todas las direcciones, en vez de seguir recta a través de la apertura.”
El principio de Huygens nos indica que si el objeto observado es menor que la longitud de onda de la luz utilizada, la luz difractará alrededor del objeto. Teniendo en cuenta la longitud de onda de la luz visible, las lupas resuelven hasta unos 600 nm.
Cuantitativamente, podemos considerar el criterio de Rayleigh,
Es la resolución, la longitud de onda de la radiación utilizada, n el índice de refracción del medio y ß un ángulo relacionado con lo paraxial que sea el sistema (depende de las aperturas utilizadas).
Por lo tanto, si queremos observar objetos con un tamaño característico menor que estos 600 nm, y dados los recientes desarrollos en nanotecnología y ciencia de materiales, es evidente que sí, tendremos que buscar una radiación con una longitud de onda menor.
En este sentido, la física cuántica nos indica que todas las partículas se comportan también como ondas (y las ondas como partículas), es la llamada dualidad onda-partícula. Los electrones, en particular, tendrán asociada una longitud de onda según la relación de Broglie:
donde h es la constante de Plank (6.63.10-34J/s) y p es el momento lineal del electrón.
Por lo tanto, la longitud de onda de los electrones dependerá de la diferencia de potencial con la que los aceleremos. En particular, si aceleramos el electrón con una diferencia de potencial de 200 kV, su longitud de onda será tan pequeña como 2.5 pm!
¿Por qué ver con electrones?
Hemos visto que los electrones parecen buenos candidatos para hacer imagen, pero podemos considerar otros tipos de radiaciones, como por ejemplo los neutrones o los rayos X.
Típicamente, en los experimentos de difracción de neutrones, los neutrones tienen una longitud de onda 1.5 - 5 Å. Por su parte, los rayos X tienen una longitud de onda del orden de = 1 Å. Por lo tanto, ¿por qué no “ver” con neutrones o rayos X? ¿Qué hace que los electrones sean tan particularmente interesantes en óptica, hasta el punto de hablar de óptica electrónica?
El hecho es que los electrones son partículas cargadas, y por lo tanto siguen la ley de Lorentz:
Por lo tanto, es posible deflectarlos con campos electromagnéticos, es decir, construir lentes para electrones, y en última instancia, microscopios.
El primer microscopio electrónico de transmisión lo construyeron Ruska y Knoll en la década de 1930, hecho por el cual recibieron el premio Nobel de física en 1986.
En la figura 3, se muestra a Ruska y Knoll con su microscopio; en la figura 4, el FEI Titan Pico, el TEM con mejorresolución actualmente.
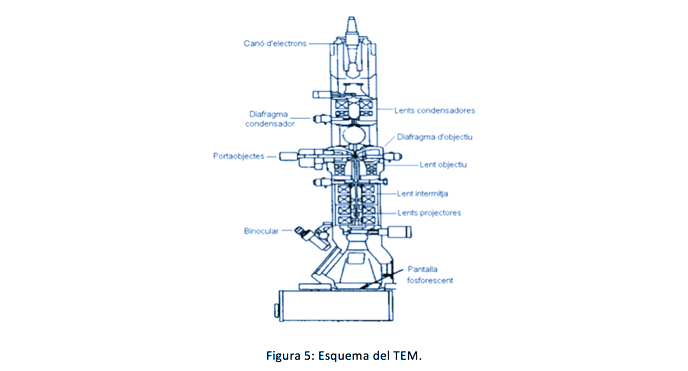
Les partes principales de un microscopio electrónico de transmisión son (figura 5):
Cañón de electrones, que es la fuente de los electrones que se acelerarán.
Lentes electromagnéticas, análogas a les lentes de un microscopio óptico.
Aperturas mecánicas, para seleccionar determinados haces, o determinadas regiones de la muestra.
Sistema de vacío, ya que el vacío es crucial en un TEM.
Como los electrones pueden ser desviados por las moléculas que pueda haber en la columna, se ha de trabajar en ultra alto vacío (del orden de 10-5 Pa).
Pantalla fluorescente, que permite observar una primera imagen de la muestra.
Sistema de registro, placa fotográfica o CCD ligada a un PC para capturar la imagen.
Como se ve en el esquema, el cañón de electrones emite el haz. A continuación se encuentran una serie de lentes convergentes:
En primer lugar, el sistema de lentes condensadoras, que modifican el haz inicial de manera que se puede controlar su ángulo de incidencia y su diámetro.
A continuación se sitúa la lente objetivo, que es la lente que forma la imagen del espécimen.
Después de la lente objetivo se encuentra la lente intermedia. Según la corriente eléctrica que se le aplique se modificará su potencia, de forma que tendrá como plano objeto el plano focal de la lente objetivo o bien el plano imagen de la lente objetivo. De esta manera se accede a dos modos de trabajo, o bien el modo difracción (plano focal) o bien el modo imagen (plano imagen).
Finalmente, se encuentran las lentes proyectoras, que amplían la imagen real o difractada.
La imagen final es recogida en la pantalla fluorescente, en una placa fotográfica o en una CCD.
Lo que limita la resolución del TEM son las aberraciones. Las lentes electromagnéticas están muy lejos de ser perfectas; si nuestros ojos presentaran las mismas aberraciones que un TEM, se nos consideraría legalmente ciegos.
Les aberraciones más importantes son el astigmatismo, la aberración esférica y la aberración cromática. El astigmatismo se corrige compensándolo con otras lentes que se encuentran en la columna.
La aberración esférica proviene del hecho que todos los puntos del frente de ondas esférico no ven la misma focal de la lente, sino que el valor de la focal depende de la distancia al eje óptico. Esto hace que la imagen de un punto no sea un punto sino un disco. Se trabaja en el plano donde el diámetro de este disco es mínimo, es el llamado disco de mínima confusión.
Finalmente, la aberración cromática proviene del hecho que los campos electromagnéticos actúan de distinta manera sobre electrones que tienen distinta energía, y, en consecuencia, distinta velocidad. Es decir, que electrones de energías (o “colores”) diferentes verán focales diferentes.
Un cristal ideal es una repetición infinita de una unidad estructural (grupo de átomos). La red de Bravais es el conjunto de puntos de un cristal desde los cuales se ve el mismo entorno atómico. Se genera todo el cristal al repetir periódicamente un cierto conjunto de átomos, que llamaremos base atómica, asociándola a cada nudo de la red de Bravais.
La red de Bravais se puede definir a partir de tres vectores de translación fundamentales, a1, a2 i a3, de manera que las posiciones, R, de los nudos de la red se obtienen a partir de combinaciones lineales de estos vectores.
T es el vector de translación.
Sólo hay 14 clases de redes de Bravais en tres dimensiones. Se obtienen combinando las diferentes operaciones de simetría de translación y simetría puntual.
Para poder entender muchos fenómenos físicos que tienen relación con la estructura periódica de los sólidos, introducimos la noción de red recíproca. La red recíproca no tiene existencia real en el cristal. Es una construcción matemática que simplifica la descripción de los fenómenos que tienen lugar en el sólido. A cada red cristalina le corresponde una red recíproca.
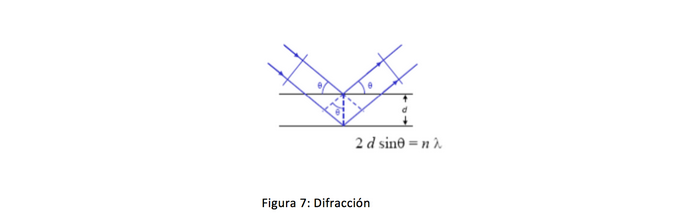
Entendemos el electrón incidente como un frente de ondas. Según el modelo de Bragg, los planos del cristal se comportan como espejos semitransparentes de manera que en cada plano se reflejan partes del mismo frente de ondas. Como no recorren el mismo camino óptico antes de superponerse de nuevo en el exterior del cristal, se producirá interferencia positiva si la diferencia de caminos ópticos es múltiple entero de la longitud de onda (nλ).
Así pues, la red cristalina se comporta como una red de difracción para el electrón incidente, lo que nos permite obtener una difracción de electrones, que nos dará información valiosa sobre la muestra de estado sólido que estemos caracterizando.
En un microscopio de transmisión de electrones, los electrones impactan contra la muestra y la imagen correspondiente se obtiene a través de la recolección de los electrones resultantes de este impacto. Algunos habrán traspasado la muestra sin ningún tipo de interacción, otros habrán traspasado pero habrán sido dispersados de forma elástica (sin pérdidas de energía) o inelástica (con pérdidas de energía), y otros pueden ser absorbidos. Además, también pueden producirse fotones como consecuencia de transiciones de energía de los electrones de los átomos que forman la muestra. Según qué tipo de señal detectemos después del impacto del haz obtendremos diferente información.
En el TEM, tenemos una lente objetivo que nos permite formar la imagen, y la muestra se sitúa en el plano objeto de la lente; la imagen de la muestra se forma en el plano imagen; además, en el plano focal imagen de la lente se encuentra el patrón de difracción. En este sentido, un conjunto de lentes en la columna (intermedia y proyectora) permiten hacer una imagen del plano imagen de la lente objetivo (modo imagen) o del plano focal imagen de la lente objetivo (modo difracción).
La apertura de selección de área, situada en el plano imagen, nos permite seleccionar una región de la muestra de la que obtener un patrón de difracción.
De forma análoga, la apertura de objetivo se encuentra en el plano de difracción. En este plano, nos permite seleccionar uno o más spots de difracción para obtener una imagen. En el caso de que seleccionemos la parte del difractograma que incluye el haz directo (los electrones que no han sido difractados) obtendremos una imagen llamada de campo claro (Bright Field), y si no lo incluimos obtendremos una imagen llamada campo oscuro (Dark Field).
En las imágenes de campo claro, veremos claras las zonas en las que no haya muestra (más intensidad del spot transmitido) mientras que en campo oscuro veremos oscuras las zonas en las que no haya muestra.
El campo oscuro nos permite obtener imágenes de defectos cristalinos y entender en qué dirección cristalográfica se dan, o estimar el grado de policristalinidad de una muestra dada.
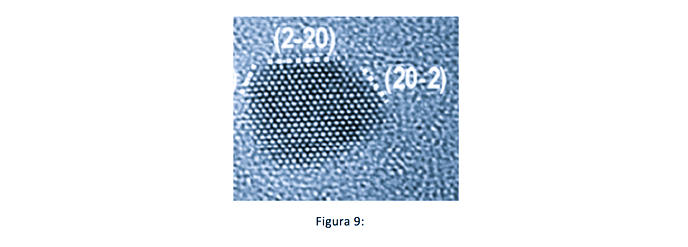
En campo claro obtenemos imágenes de la morfología general de la muestra, por ejemplo. Un caso particular del campo claro son las imágenes de alta resolución, en las que vemos la periodicidad de los planos cristalinos.
MATERIAL EXTRAIDO DE Técnicas Microscópicas de Caracterización (Universitat de Barcelona)
Microscopía Electrónica de Transmisión (TEM)
Williams, David B., Carter, C. Barry, Transmission Electron Microscopy: A Textbook for Materials Science, Springer Verlag, New York Inc., 2009.
Kittel, Charles, Introduction to Solid State Physics, Wiley, 2004.